In the last post I demonstrated probe distributions under six insertion schemes: linear probing, quadratic probing, double hashing, and their robin hood hashing variants. Knowing the probe distribution of insertion is useful for static hash tables, but does not model the hash table with frequent updates. Therefore I made some experiments for such scenario, and found the results are very interesting.
Same disclaimer. I now work at google, and this project (OPIC including the hash table implementation) is approved by google Invention Assignment Review Committee as my personal project. The work is done only in my spare time on my own machine, and does not use and/or reference any of the google internal resources.
Deletion in open addressing schemes
In most open addressing schemes, deletion is done by marking the bucket with a tombstone flag. During the next insertion, both empty bucket and tombstone bucket can hold new items. During look ups, seeing an empty bucket means the key was not found, but if you saw a tombstone bucket you must continue probing. If too many items got deleted and causes the load smaller than a threshold, shrink the hash table and re-insert the non-tombstone items.
Table with high insertion/deletion rate
Consider the following: you are maintaining a large key value store which uses hash table internally. The key value store has many keys inserted and deleted frequently, but the total keys remains the same (limited by capacity or ttl). Let’s assume all keys have equal probability to get deleted. The keys with low probing count would eventually get deleted at sometime, while the newly inserted key may occur with high probing count because the table is always under high load. An interesting question rises:
- Will the probe number continue growing?
- Or the probe number converges to certain distribution?
I yet to see mathematical analysis on this problem. If you know a good reference, please leave a comment. Finding the formal bound were too hard for me, so I designed a small experiment to understand the effect. The experiment will have ten rounds. In the first round, insert 1M items. In the next nine rounds, delete an item and insert a new item for 1M times. I only tested this experiment on quadratic probing scheme and robin hood with quadratic probing.
Quadratic probing with deletion
Quadratic probing is used in dense hash map. This is one of the
fastest hash table with wide adoption, therefore worth the study.
For this experiment I didn’t use dense hash map, instead I wrote
a small C program with same probing algorithm and record the probe counts.
The chart below is a histogram of probe count for quadratic probing.
Each line is the distribution of probes of different rounds; 00 is
insertion only round, and others have pair of deletion and insert.
Each round have 1M items inserted and/or deleted. The table is under
80% load.
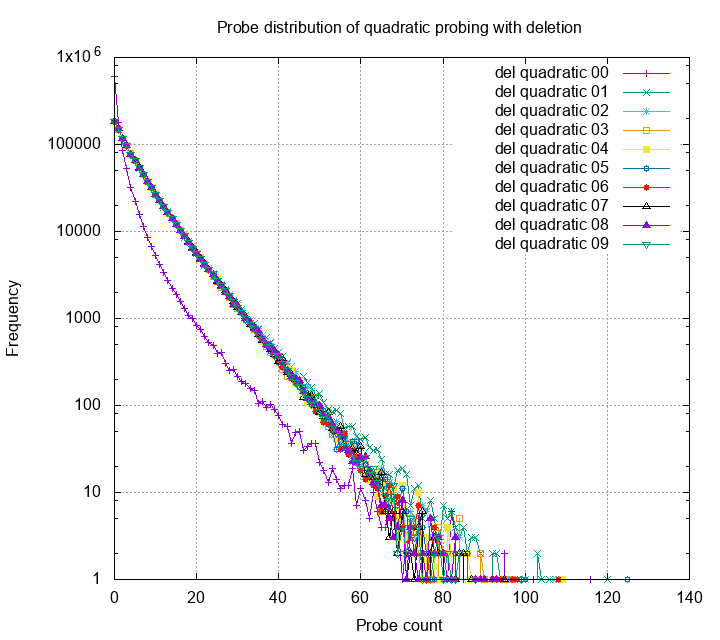
Surprisingly, the probe histogram converges to a shape after one round. This means that the hash table performance will drop after one round of replacing all the elements, but will reach to a steady state and stop getting worse. The shape of the steady distribution looks like a exponential distribution. I wonder can we use this property and further derive other interesting properties?
Robin hood hash with deletion
In the robin hood hashing thesis the author conjectured that having deletion would cause the mean of probe count increase without bound, but the variance would remain bounded by small constant.
Paul Khuong and Emmanuel Goossaert pioneered to approach this problem. The intuition is fill the deleted bucket by scanning forward candidate buckets. See Emmanuel’s post for more detail.
Inspired by their robin hood linear probing deletion, I created one for robin hood quadratic probing. The idea is similar, except the candidates are not limited to its neighbors. I have to scan through possible candidates from largest probe number, and check is the candidate valid to fill the spot. There are some other tricks I did to make sure the iteration done in deletion is bounded, but isn’t important in this post.
The probe distribution using this idea is shown as follows:
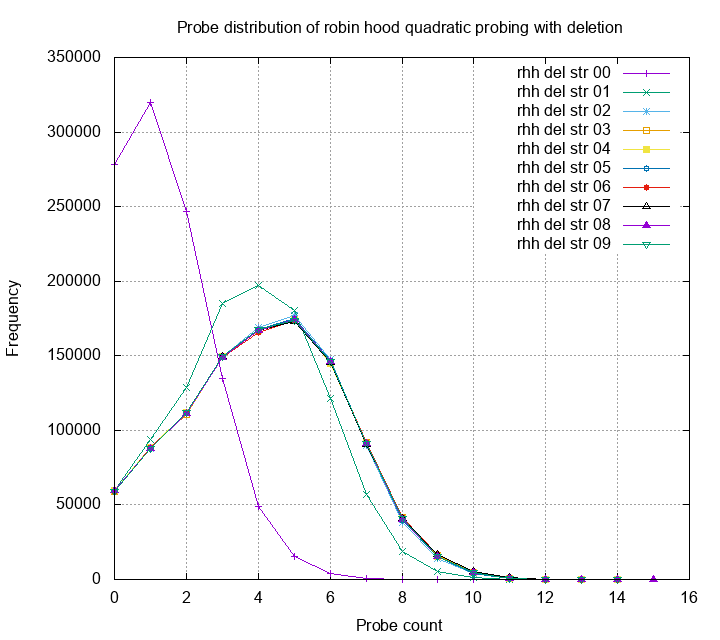
The result is also very good. Both the mean and variance is smaller than naive quadratic probing. Luckily, the conjecture of unbounded mean wasn’t true, it converges to a certain value! Recall from last post; we want to know what is the worst case probe (< 20 for 1M inserts) and the average case. Even with lots of inserts and deletes, the mean is still in constant bound, and the worst case is not larger than O(log(N)).
How about robin hood hashing without the re-balancing strategy? Again, the results blows my mind:
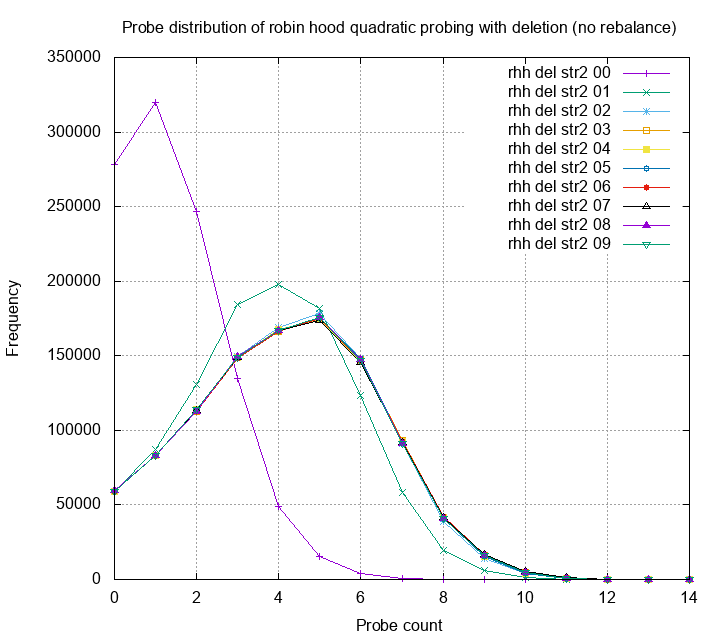
It’s actually very identical to my carefully designed deletion method. When I first see the experiment result, I was quite shocked. I can do nothing but to accept the experiment result, and adapt new implementation. In my journey of optimizing hash tables, I found clever ideas often failed (but not always!). Finding a good combination of naive and clever ideas for good performance is tough. I did it by doing exhaustive search of different combinations, then carefully measure and compare.
In OPIC robin hood hashing I initially only interested at building static hash table with high load. However, after this experiments I concluded that robin hood hashing has good potential for dynamic hash table as well.
Aggregated stats
Last but not least, let’s look at mean and variance for each method and each round.
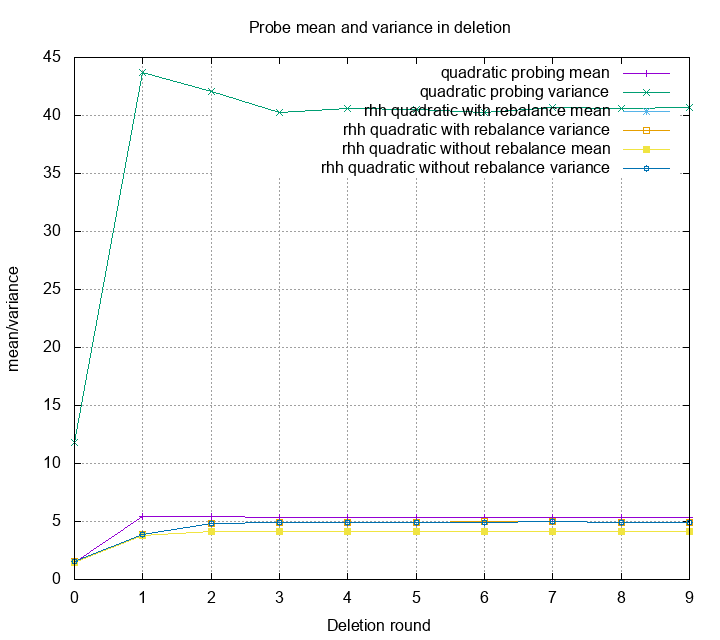
The mean of quadratic probing and robin hood quadratic probing actually doesn’t differ by much. Only a little bit after first round. The difference of variance is huge because that’s what robin hood hashing is designed for.
Summary
In the first two post of learn hash table series, we examined probe distributions of various methods and scenarios. In the next post I’ll show how these distribution reflects on actual performance. After all, these experiments and study were meant to leads to better engineering result.